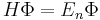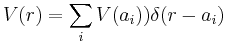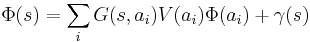Discrete delta-potential method

The discrete delta potential method is a combination of both numerical and analytic method used to solve the Schrödinger equation the main feature of this method is to obtain first a discrete approximation of the potential in the form:

$V(r)=\sum_{i}V(a_{i}))\delta(r-a_{i})$

where the i index runs over several discrete chosen points of the continuous potential, with this we can solve the SE in the form:

$\Phi(s)=\sum_{i}G(s,a_{i})V(a_{i})\Phi(a_{i})%2B\gamma(s)$

Where G(s, r) is the Green function associated to the free particle Hamiltonian H0, setting s=ai for every i would give a system of linear equation.

For a better approach if potential V(x) is weak we can treat the continuous part of the potential and perform perturbation theory to obtain a better wave function.

If the points are equidistant :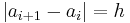 $|a_{i%2B1}-a_{i}|=h$ the wave function will depend on h so performing the solution to several h and extrapolating to the value h=0 we could obtain the solution of SE (Schrödinger equation).

This method is valuable when we cannot perform perturbation theory and need some analytic approach to the solution of SE: $H\Phi=E_{n}\Phi$